树链剖分 | guanghechen

算法简介
¶

树链剖分是将树上的节点映射到一段连续的区间中，使得树上任意一条路径能用不超过 $O (\log N)$ 段连续区间表示。这样，利用线段树就可以在 $O (\log^{2} N)$ 的时间复杂度对树上任意路径上的节点进行进行维护和查询了。

算法原理
¶

$s i z (u)$ : 以 $u$ 为根的子树的节点数
$s o n (u)$ : $u$ 的子节点中 $s i z$ 值最大的节点
重边: $u$ 与 $s o n (u)$ 的连边
轻边: $u$ 与除 $s o n (u)$ 外其它子节点的连边
重链: 由重边连成的路径

定理1
¶

如果 $(u, v)$ 是一条轻边，那么 $s i z (v) < \frac{s i z (u)}{2}$ .

因为 $(u, v)$ 是一条轻边，所以 $u$ 还有一个由重边相连的儿子 $s o n (u)$ .
若 $s i z (v) ⩾ \frac{s i z (u)}{2}$ ，根据定义，有 $s i z (s o n (u)) ⩾ s i z (v) ⩾ \frac{s i z (u)}{2}$ .
与 $s i z (u) ⩾ s i z (v) + s i z (s o n (u)) + 1 > 2 \times s i z (v)$ 矛盾。
故， $s i z (v) < \frac{s i z (u)}{2}$ 。

定理2
¶

任意非根节点 $u$ 到根节点的路径上，轻边+重链总数不超过 $O (\log_{2} N)$ .

不难证明，最多会遇到 $\log_{2} N$ 条轻边。
因为从根节点到 $u$ 的路径中，每遇到一条轻边，节点个数就会减半，
所以轻边的数目不超过 $\log_{2} N$ .
而整条路径上 $\log_{2} N$ 条轻边最多隔开 $\log_{2} N + 1$ 条重链。
故，轻边+重链总数不超过 $O (\log_{2} N)$ 。

由定理2 可知当我们将一棵树沿着重链剖分后，将重链依次映射到一段连续的区间后，就可以将任何一条到根的链分成 $\log N$ 段连续区间了。也就是用 $\log N$ 条重链的覆盖这一条路径。

算法实现
¶

$f a t (u)$ : $u$ 的父亲
$s o n (u)$ : $u$ 的子节点中 $s i z$ 值最大的节点
$d e p (u)$ : $u$ 的深度，根节点深度为 $1$
$s i z (u)$ : 以 $u$ 为根的子树的节点数
$p o s (u)$ : $u$ 在连续区间的映射值
$t o p (u)$ : $u$ 所在重链的顶端节点

求出 $s i z, d e p, s o n, f a t$

dfs1.cpp

1
2
3
4
5
6
7
8
9
10
11
12
int fat[MAXN], son[MAXN], dep[MAXN], siz[MAXN];
void dfs(int o, int f, int d) {
  fat[o] = f; son[o] = 0;
  dep[o] = d; siz[o] = 1;
  for (int u = from[o]; u; u = nxt[u]) {
    int v = to[u];
    if (v == f) continue;
    dfs(v, o, d+1);
    siz[o] += siz[v];
    if (siz[son[o]] < siz[v]) son[o] = v;
  }
}

求出 $t o p, p o s$ ，

dfs2.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int top[MAXN], pos[MAXN], dfs_clock;
void dfs(int u, int t) {
  pos[u] = ++dfs_clock;
  top[u] = t;
  if (!son[u]) return;

  // u 与 son(u) 在同一条重链上，故重链的顶端节点相同
  dfs(son[u], t);

  for (int i = from[u]; i; i = nxt[i]) {
    int v = to[i];

    // u 的其它非 son(u) 子节点为新的重链的顶端节点
    if (v != fat[u] && v != son[u]) dfs(v, v);
  }
}

树链剖分完了！！怎么用呢？如下图所示，粗线表示重边，虚线表示轻边，黑色数字为节点编号，紫色数字为边编号。图中的 0 节点为一虚拟节点，引进它是方便理解下文 ^[1]。每条边上的紫色数字表示箭头所指的节点的 $p o s$ 值。

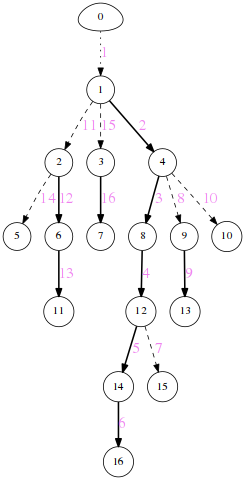
对于树上的两个节点 $u$ ， $v$ ，若它们的最近公共祖先（LCA）为 $w$ ；那么，如果我们想要对路径 $(u, v)$ 上的所有节点进行一个操作，只需要让 $u$ , $v$ 同时沿着各自的祖先节点走，并在 $w$ 处相遇就可以了。

$t o p$ 是为了加速往上走的过程；但是不难发现，由于每次可能不仅走一步，如果 $u$ 和 $v$ 同时行动的话，很可能会错过 $w$ ！为了解决这个问题，可以总是让 $d e p (t o p)$ 值大的点先走（想一想，为什么）。

不妨假设 $d e p (t o p (u)) ⩾ d e p (t o p (v))$
若 $t o p (u) \neq t o p (v)$ ，则得到一段连续的映射区间 $[p o s (t o p (u)), p o s (u)]$ ；让 $u$ 走到 $f a t (t o p (u))$
否则 $t o p (u) = t o p (v)$ ，即 $u$ 和 $v$ 在同一条重链中。显然， $w = {x | d e p (x) = min {d e p (y) | y \in {u, v}}, x \in {u, v}}$ ，得到一段连续的映射区间 $[p o s (w), p o s ({u, v} - {w})]$

由于每次走到 $f a t (t o p)$ ，可以放心的把轻边当做长度为 $0$ 的重链来处理。比如，我们现在要访问 节点6 --> 节点15 的路径：

$u$ 走到 12，得到一段连续的映射区间 $[7, 7]$
$u$ 走到 1，得到一段连续的映射区间 $[2, 3]$
$v$ 走到 2，得到一段连续的映射区间 $[12, 12]$
$v$ 走到 1，得到一段连续的映射区间 $[11, 11]$
$t o p (u) = t o p (v)$ ，得到一段连续的映射区间 $[1, 1]$ ；相遇，终止算法

所以，我们在映射区间里依次对 ${[7, 7], [2, 3], [12, 12], [11, 11], [1, 1]}$ 进行操作就好了。

update.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void update(int L, int R) {
  while (top[L] != top[R]) {
    // 让 dep 大的走
    if (dep[top[L]] < dep[top[R]]) swap(L, R);

    // 得到连续映射区间 [l,r]
    int l = pos[top[L]], r = pos[L];

    // 对 [l,r] 进行操作
    fun(l, r);

    L = fat[top[L]];
  }
  if (dep[L] > dep[R]) swap(L, R);
  fun(pos[L], pos[R])
}

小记
¶

上文中讨论的是对 $(u, v)$ 路径上的所有节点进行操作。若信息全维护在边上，即要对 $(u, v)$ 路径上的所有边进行操作，则仅需在 $d e p (u) = d e p (v)$ 时，执行的区间改成 $[p o s (s o n (u)), p o s (v)]$ 就行了。

树链剖分

算法简介¶

算法原理¶

定理1¶

定理2¶

算法实现¶

小记¶

Related¶