HDU-5574 Colorful Tree 解题报告（原 2015-上海区域赛-C）

题意简述
¶

一棵 $N$ 个节点的树，节点编号 $1 \sim N$ ，且根节点编号始终为 $1$ 。初始时，节点 $i$ 的颜色为 $c_{i}$ 。执行 $M$ 次操作，每次操作为下述操作之一：

0 u c: 将以 $u$ 为根节点的子树中所有的节点颜色染成 $c$
1 u: 输出以 $u$ 为根节点的子树中颜色种数

数据范围： $1 ⩽ T ⩽ 100$ ， $1 ⩽ N, M ⩽ 10^{5}$ , $1 ⩽ c_{i} ⩽ N$ 。

题目简析
¶

不能想到要用线段树进行查询，问题关键在于如何建树。如果直接用 DFS 序来表示树中的一段区间的话，维护颜色就举步维艰了，因为查询是一棵子树的颜色种数，普通的区间标记根本就无能为力。只好另谋出路。

注意到，在树中一个节点的颜色只会对其及祖先节点有贡献。具体地，一个节点的颜色更改可以视作将原来的颜色删除，再添加新的颜色。这样的话，删除颜色就对该节点及其祖先节点贡献 $- 1$ ；添加颜色则 $+ 1$ 。但是，不难发现，这里存在有一个问题，如下图（先仅考虑 orange 对祖先节点的贡献）:

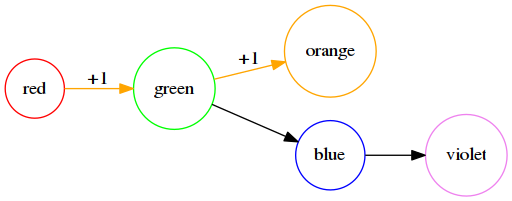
上图中，orange 对节点 orange、green 及 red 都有一个贡献值。但是，如果我们要把 violet 的颜色改成 orange 的话，则从 violet -> red 这一条链中：

删除颜色 所有节点的贡献 -1
添加颜色 只对 violet、blue 两个节点 +1。因为，节点 red、green 已被 orange 这个颜色更新过了。

算法
¶

不难想到，当修改一个节点 $i$ 的颜色 $c_{i}$ 时，我们仅需修改所有与 $c_{i}$ 颜色相同的节点与 $i$ 的最近公共祖先（所有与 $i$ 构成的最近公共祖先中的距离 $i$ 最近的祖先） $g_{i}$ 到 $i$ 这条路径的所有的节点（包括 $i$ ，但不包括 $g_{i}$ ）即可。如下图（仅考虑将 violet 颜色修改成 orange 这种情况对祖先节点的贡献）：

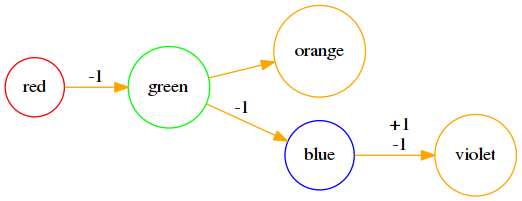
如何找到 $g_{i}$ 呢？假设节点 $i$ 在这棵树先序遍历序列中位置为 $f_{i}$ 。记节点 $j$ 和 $k$ 是所有和节点 $i$ 的颜色相同的节点中，先序遍历中最靠近 $i$ 的两个节点。即满足 $c_{j} = c_{k} = c_{i}$ ，且 $f_{\dots} < f_{j} < f_{i} < f_{k} < f_{\dots}$ .

那么， $f_{g_{i}} = min {f_{L C A (i, j)}, f_{L C A (i, k)}}$ 。其中， $L C A (i, j)$ 表示节点 $i$ 、 $j$ 的最近公共祖先。

所以，我们只要对每一种颜色开一棵平衡树，键值为节点的 dfs 序。然后 lower_bound, upper_bound 一下就可以找到 $j$ ， $k$ 了。

至于链上的操作树链剖分就可以了。

所以当我们执行一次 操作0 时，要把 $u$ 的子树中所有的颜色删掉，然后仅给 $u$ 添加新的颜色 $c$ 。注意到这样一来，一个节点颜色 $c_{i}$ 就是距它最近的有颜色的祖先 ^[1] 的颜色了。

同时，这样一来当前节点颜色并非总是对自己贡献 $+ 1$ ，因为我们始终只考虑了 $u$ -> $g (u)$ 这条路径上的节点；而 $u$ 的子孙节点其实是有颜色的，且均为 $c$ 。所以，查询时如果发现当前节点颜色未在子孙节点中出现，答案 $+ 1$ 。

判断当前节点颜色是否在子孙节点中出现有一个小技巧：

1
2
3
4
5
6
int flag = 0;
int c = getColor(u);
if (c) {
    it = lower_bound(s[c].begin(), s[c].end(), st[u]);
    if (it == s[c].end() || *it > ed[u]) flag = 1;
}

复杂度分析
¶

由于删除一个节点的复杂度为 $O (\log^{2} N)$ （树链剖分有一个 $\log$ )，我们最多添加 $M$ 个节点，因此时间复杂度为 $O ((M + N) l o g^{2} N)$ 。

空间复杂度: $O (N)$
时间复杂度: $O ((M + N) l o g^{2} N)$

AC 代码：

hdu.5574.cpp | 249 lines.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
#include <bits/stdc++.h>
using namespace std;

#define lc (o << 1)
#define rc (o << 1 | 1)
#define lson lc, lft, mid
#define rson rc, mid + 1, rht
#define MID(L, R) ((L) + (R) >> 1)

const int MAXN = 1e5 + 10;
const int root = 1;

int N;

int from[MAXN], nxt[MAXN << 1], to[MAXN << 1], edge_siz;
void addEdge(int u, int v) {
  to[++edge_siz] = u;
  nxt[edge_siz] = from[v];
  from[v] = edge_siz;
}

int father[MAXN], son[MAXN], dep[MAXN], siz[MAXN];
void dfs(int o, int f, int d) {
  father[o] = f;
  son[o] = 0;
  dep[o] = d;
  siz[o] = 1;

  for (int u = from[o]; u; u = nxt[u]) {
    int v = to[u];
    if (v == f) continue;

    dfs(v, o, d + 1);
    siz[o] += siz[v];
    if (siz[son[o]] < siz[v]) son[o] = v;
  }
}

int top[MAXN], st[MAXN], ed[MAXN], id[MAXN], dfs_clock;
void dfs(int o, int t) {
  st[o] = ++dfs_clock;
  id[dfs_clock] = o;
  top[o] = t;

  if (son[o]) {
    dfs(son[o], t);
    for (int u = from[o]; u; u = nxt[u]) {
      int v = to[u];
      if (v != father[o] and v != son[o]) dfs(v, v);
    }
  }

  ed[o] = dfs_clock;
}

int lca(int u, int v) {
  while (top[u] != top[v]) {
    if (dep[top[u]] < dep[top[v]]) swap(u, v);
    u = father[top[u]];
  }
  return dep[u] < dep[v] ? u : v;
}

pair<int, int> T[MAXN << 2];
int color[MAXN];

void pushdown(int o) {
  T[lc].first += T[o].first;
  T[rc].first += T[o].first;
  T[o].first = 0;
}

void build(int o, int lft, int rht) {
  T[o].first = 0;
  if (lft == rht) {
    T[o].second = color[id[lft]];
  } else {
    int mid = MID(lft, rht);
    build(lson);
    build(rson);

    T[o].second = 1;
  }
}

void update(int o, int lft, int rht, int L, int R, int V) {
  if (L <= lft and rht <= R) {
    T[o].first += V;
  } else {
    int mid = MID(lft, rht);
    if (L <= mid) update(lson, L, R, V);
    if (R > mid) update(rson, L, R, V);
  }
}

int query(int o, int lft, int rht, int P) {
  if (lft == rht) return T[o].first;
  if (T[o].first) pushdown(o);

  int mid = MID(lft, rht);
  if (P <= mid) return query(lson, P);
  return query(rson, P);
}

void updatePath(int u, int v, int w) {
  while (top[u] != top[v]) {
    if (dep[top[u]] < dep[top[v]]) swap(u, v);
    update(1, 1, N, st[top[u]], st[u], w);
    u = father[top[u]];
  }
  if (dep[u] > dep[v]) swap(u, v);
  update(1, 1, N, st[u], st[v], w);
}

set<int> s[MAXN];
set<int>::iterator it;

int lowerColor(int o, int lft, int rht, int L, int R) {
  if (!T[o].second) return 0;
  if (lft == rht) return T[o].second;

  int mid = MID(lft, rht);
  int rcolor = 0;
  if (R > mid) rcolor = lowerColor(rson, L, R);
  return (!rcolor and L <= mid) ? lowerColor(lson, L, R) : rcolor;
}

int getColor(int x) {
  while (top[x] != top[root]) {
    int ret = lowerColor(1, 1, N, st[top[x]], st[x]);
    if (ret) return ret;
    x = father[top[x]];
  }
  return lowerColor(1, 1, N, st[root], st[x]);
}

void maintain(int x, int c, int op) {
  if (~op) s[c].insert(st[x]);
  it = upper_bound(s[c].begin(), s[c].end(), st[x]);
  int pr = 0, su = 0;

  if (it != s[c].end()) {
    su = lca(x, id[*it]);
  }
  --it;
  if (it != s[c].begin()) {
    --it;
    pr = lca(x, id[*it]);
  }

  if (!pr and !su)
    updatePath(1, x, op);
  else {
    if (st[pr] < st[su]) pr = su;

    updatePath(pr, x, op);
    updatePath(pr, pr, -op);
  }

  if (op == -1) s[c].erase(st[x]);
}

void remove(int o, int lft, int rht, int L, int R) {
  if (!T[o].second) return;
  if (lft == rht) {
    maintain(id[lft], T[o].second, -1);
    T[o].second = 0;
  } else {
    int mid = MID(lft, rht);
    if (L <= mid) remove(lson, L, R);
    if (R > mid) remove(rson, L, R);

    T[o].second = T[lc].second or T[rc].second;
  }
}

void insert(int o, int lft, int rht, int P, int C) {
  if (lft == rht) {
    maintain(id[lft], C, 1);
    T[o].second = C;
  } else {
    int mid = MID(lft, rht);
    if (P <= mid)
      insert(lson, P, C);
    else
      insert(rson, P, C);

    T[o].second = 1;
  }
}

void init() {
  memset(from, 0, sizeof from);
  edge_siz = 0;

  for (int i = 1; i <= N; ++i) s[i].clear();
  dfs_clock = 0;
}

void work() {
  int T_T, Q, u, v, w, cmd;

  scanf("%d", &T_T);
  for (int kase = 1; kase <= T_T; ++kase) {
    printf("Case #%d:\n", kase);

    scanf("%d", &N);
    init();
    for (int i = 1; i < N; ++i) {
      scanf("%d%d", &u, &v);
      addEdge(u, v);
      addEdge(v, u);
    }
    for (int i = 1; i <= N; ++i) scanf("%d", color + i);

    dfs(root, -1, root);
    dfs(root, 1);
    build(1, 1, N);

    for (int i = 1; i <= N; ++i) maintain(i, color[i], 1);

    scanf("%d", &Q);
    while (Q--) {
      scanf("%d", &cmd);
      switch (cmd) {
      case 0:
        scanf("%d%d", &u, &v);
        remove(1, 1, N, st[u], ed[u]);
        insert(1, 1, N, st[u], v);
        break;
      case 1:
        scanf("%d", &u);
        int flag = 0;
        int c = getColor(u);
        if (c) {
          it = lower_bound(s[c].begin(), s[c].end(), st[u]);
          if (it == s[c].end() || *it > ed[u]) flag = 1;
        }
        printf("%d\n", query(1, 1, N, st[u]) + flag);
        break;
      }
    }
  }
}

int main() {
  work();
  return 0;
}

小记
¶

据说正解是 $O (N \log N)$ 的，本蒟蒻表示不会。
多谢小小兰学长的指教。

题意简述¶

题目简析¶

算法¶

复杂度分析¶

小记¶

Related¶

题意简述
¶

题目简析
¶

算法
¶

复杂度分析
¶

小记
¶

Related
¶