精确覆盖问题和 DLX 算法
前言
¶很早就想要补一下舞蹈链和精确覆盖算法,却一直各种拖延,趁着最近有空,又重新翻开了刘汝佳的书。大学的时候看过几次,甚至照着书里的思路手敲了一遍并通过了例题,但对于算法的原理一直有些不求甚解。很早以前,一位同学告诉我说“现在看不懂的东西不用勉强,以后慢慢就会懂了”,后来也真的在不断印证这句话;但我很担心随着年纪的增长,记忆力和学习能力不断退化之后,恐怕这个 flag 会逐渐倒下。所以趁着眼下尚能理解进去,尽量用自己的语言做一下记录。
精确覆盖问题
¶有一些由整数 $1 \sim n$ 中的数字组成的集合 $S_1, S_2, \cdots, S_m$,要求选择若干个集合 $S_i$,使得 $1 \sim n$ 中每个整数都在选出的集合中的某个出现且恰好仅出现一次。举个栗子:
不妨假设 $n=7, m=6$,集合为:
$$\begin{aligned} S_1&=\lbrace 1, 4, 7 \rbrace\\ S_2&=\lbrace 1, 4 \rbrace\\ S_3&=\lbrace 4,5,7 \rbrace\\ S_4&=\lbrace 3, 5, 6 \rbrace\\ S_5&=\lbrace 2, 3, 6, 7 \rbrace\\ S_6&=\lbrace 2, 7 \rbrace\\ \end{aligned}$$则一个精确覆盖为 $\lbrace S_2, S_4, S_6 \rbrace$,因为 $\lbrace 1, 4 \rbrace$, $\lbrace 3, 5, 6 \rbrace$, $\lbrace 2, 7 \rbrace$ 无重复、无遗漏地包含了 $1 \sim 7$ 中的所有整数。
我们可以用一个 $m \times n$ 的 $01$ 矩阵来表示集合,其中,$0$ 表示不包含,$1$ 表示包含。比如第 $(i, j)$ 个位置若为 $0$,则说明 $S_i$ 中不包含 $j$。上文中的栗子用矩阵表示如下所示:
| $$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ |
|---|---|---|---|---|---|---|---|
| $S_1$ | $1$ | $0$ | $0$ | $1$ | $0$ | $0$ | $1$ |
| $S_2$ | $1$ | $0$ | $0$ | $1$ | $0$ | $0$ | $0$ |
| $S_3$ | $0$ | $0$ | $0$ | $1$ | $1$ | $0$ | $1$ |
| $S_4$ | $0$ | $0$ | $1$ | $0$ | $1$ | $1$ | $0$ |
| $S_5$ | $0$ | $1$ | $1$ | $0$ | $0$ | $1$ | $1$ |
| $S_6$ | $0$ | $1$ | $0$ | $0$ | $0$ | $0$ | $1$ |
则精确覆盖问题可重新表述为:在一个 $m \times n$ 的 $01$ 矩阵中,选择若干行,对这些行做向量加法,得到的结果为 $(1, 1, \cdots, 1)$。即:
- 选出的行里,不存在某列同时在两行中值均为 $1$;
- 所有选出的行叠加在一起的结果覆盖所有列(每一列的值都不为 $0$)。
算法 X
¶算法 X(Algorithm X),其实就是回溯,可能是专门针对覆盖问题提出的算法吧。算法描述如下:
每次选择一个没有被删除列,然后枚举该列为 $1$ 的所有行,尝试删除这些行,递归搜索后再恢复这些行。尝试删除行时,还要将该行中所有值为 $1$ 的列也一并删除[1],恢复时也同样。
若没有可以选择的列了(即所有列都被删除了),说明已经找到一个精确覆盖的解了[2];若还有列但是没有行了[3]说明原问题无解。
舞蹈链
¶舞蹈链(Dancing Link),一种支持快速删除、恢复列和行的数据结构。
舞蹈链是一个十字型双向链表结构,链表中的每个节点对应上述 $01$ 矩阵中的一个 $1$。另外还有 $n+1$ 个虚拟节点,其中每列最上方一个虚拟节点作为该列链表的头指针,而所有虚拟节点的最前方有一个虚拟节点,作为虚拟节点的头指针,它也是舞蹈链的头指针。如下图所示(图片来源于网络):
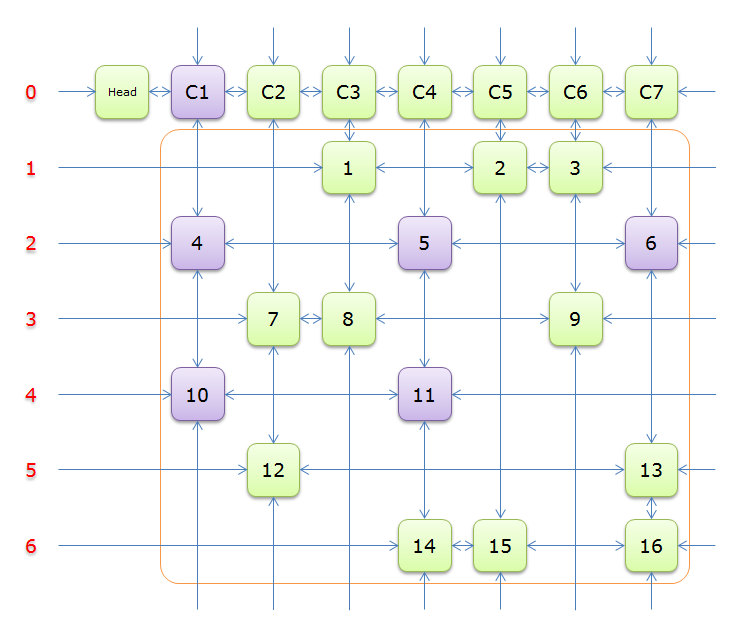
使用四个数组 $L$, $R$, $U$, $D$ 分别表示舞蹈链中节点的左、右、上、下四个方向的指针,下标为节点的编号;同时列编号作为该列的虚拟节点,$0$ 表示舞蹈链的头指针对应的虚拟节点。
删除行:只需要修改将该行中所有节点的上下行的下、上指针互指就好了。
dancing-link.01.ts12345// 设要删除的某行中某个节点编号为 R[i]for (let j = R[i]; j !== i; j = R[j]) {U[D[j]] = U[j]D[U[j]] = D[j]}恢复行:只需要将该行中所有节点的上下行的下、上指针分别指向该该节点就好了。
dancing-link.01.ts12345// 设要删除的某行中某个节点编号为 R[i]for (let j = R[i]; j !== i; j = R[j]) {U[D[j]] = jD[U[j]] = j}删除列和恢复列也类似,此处略去。
DLX 算法
¶使用了舞蹈链的算法 X 通常被称为 DLX 算法。此处给出 DLX 算法的 Typescript 实现[4]。
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240/** * The algorithm X that applied the dancing-link, it is also called as "DLX". * It is used to solve the exact-cover problem. * * Dancing-link: A cross doubly linked list, each column has a virtual node as * the head pointer, and at the top of all virtual nodes there is an additional * virtual node as the head pointer of the virtual node, which is also the head * pointer of the entire dancing-link. In the implementation of using an array * to simulate a linked list, the virtual node is represented by a column * number, and the head pointer of the dancing-link can be represented by 0. * * @see https://me.guanghechen.com/post/algorithm/dlx/ */export interface DLX { /** * Initialize the dancing-link. * @param totalColumns number of columns */ init(totalColumns: number): void
/** * Release memory variables. */ destroy(): void
/** * Add a row to the dancing-link. * * It should be noted that after solving the exact-cover problem, the * result is a list of selected row numbers, so the row number should be * specified as a value that can carry information. * * @param r the row number * @param columns columns on the row */ addRow(rowNo: number, columns: ReadonlyArray<number>): void
/** * Try to find a precise coverage. * * When a solution is found, return the row numbers of all selected rows, * otherwise return null. */ solve(): number[] | null}
/** * Generate an object that encapsulates the DLX algorithm. * * @param MAX_N maximum number of nodes in the dancing-link * @returns */export function createDLX(MAX_N: number): DLX { // The number of nodes in the dancing-link (including the virtual nodes on // the column). let sz: number
// the number of columns in the dancing-link. let totalColumns: number
const selectedRowNos: number[] = new Array(MAX_N) // list of row numbers of selected rows let countOfSelectedRows: number // the number of selected rows
const count: number[] = new Array(MAX_N) // lhe number of nodes of a column in the dancing-link const row: number[] = new Array(MAX_N) // the row number of a node in the dancing-link const col: number[] = new Array(MAX_N) // the column number of a node in the dancing-link const L: number[] = new Array(MAX_N) // left pointer of cross-link list const R: number[] = new Array(MAX_N) // right pointer of cross-link list const U: number[] = new Array(MAX_N) // up pointer of cross-link list const D: number[] = new Array(MAX_N) // down pointer of cross-link list return { init, destroy, addRow, solve }
/** * @see DLX#init * @public */ function init(_totalColumns: number): void { totalColumns = _totalColumns sz = _totalColumns + 1
// Resize arrays. if (selectedRowNos.length < sz) { selectedRowNos.length = sz count.length = sz row.length = sz col.length = sz L.length = sz R.length = sz U.length = sz D.length = sz }
for (let i = 0; i < sz; ++i) { L[i] = i - 1 R[i] = i + 1 U[i] = i D[i] = i } R[_totalColumns] = 0 L[0] = _totalColumns
count.fill(0, 0, sz) }
/** * @see DLX#destroy * @public */ function destroy(): void { selectedRowNos.length = 0 count.length = 0 row.length = 0 col.length = 0 L.length = 0 R.length = 0 U.length = 0 D.length = 0 }
/** * @see DLX#addRow * @public */ function addRow(r: number, columns: ReadonlyArray<number>): void { const first = sz for (let i = 0; i < columns.length; ++i, ++sz) { const c = columns[i] row[sz] = r col[sz] = c count[c] += 1
// Connect left and right nodes L[sz] = sz - 1 R[sz] = sz + 1
// Connect top and bottom nodes, // c is the virtual node on the c-th column, and is also the head pointer // of the linked list of the column, so at this time U[c] is the last // element of the column D[sz] = c D[U[c]] = sz U[sz] = U[c] U[c] = sz }
// Since this is a circular linked list, the first and last columns of the // current row are connected to each other. R[sz - 1] = first L[first] = sz - 1 }
/** * @see DLX#solve * @public */ function solve(): number[] | null { if (!algorithmX(0)) return null return selectedRowNos.slice(0, countOfSelectedRows) }
/** * Remove a column from the dancing-link. * @param c column number * @private */ function removeColumn(c: number): void { L[R[c]] = L[c] R[L[c]] = R[c] for (let i = D[c]; i !== c; i = D[i]) { for (let j = R[i]; j !== i; j = R[j]) { U[D[j]] = U[j] D[U[j]] = D[j] count[col[j]] -= 1 } } }
/** * Restore a previously deleted column * @param c column number * @private */ function restoreColumn(c: number): void { for (let i = U[c]; i !== c; i = U[i]) { for (let j = L[i]; j !== i; j = L[j]) { count[col[j]] += 1 U[D[j]] = j D[U[j]] = j } } L[R[c]] = c R[L[c]] = c }
/** * Algorithm X. * * Recursively solve the problem of precise coverage, enumerate which rows are * selected in the recursive process, remove the selected rows and all the * columns on the rows, and restore these rows and columns during the * backtrack. * * @param dep recursion depth * @private */ function algorithmX(dep: number): boolean { // Find a solution when the dancing-link is empty. if (R[0] === 0) { // Record the length of the solution. countOfSelectedRows = dep return true }
/** * Optimization: Find the column with the least number of nodes, and try to * cover from this column. */ let c = R[0] for (let i = R[0]; i !== 0; i = R[i]) { if (count[i] < count[c]) c = i }
// Remove this column. removeColumn(c) for (let i = D[c]; i !== c; i = D[i]) { selectedRowNos[dep] = row[i] for (let j = R[i]; j !== i; j = R[j]) removeColumn(col[j])
// Recursively processing. if (algorithmX(dep + 1)) return true
// Backtrack. for (let j = L[i]; j !== i; j = L[j]) restoreColumn(col[j]) } // Backtrack. restoreColumn(c)
return false }}
我把它封装在了 @algorithm.ts/dlx 中,你可以通过 npm 包导入它:
12345678910111213import { createDLX } from 'algorithm.ts/dlx'
// 创建一个基于至多有 1000 个节点的舞蹈链的 dlx 算法const dlx = createDLX(1000)
// 初始化 dlx 算法,总共有 1000 列dlx.init(1000)
// 添加行,此处为伪代码dlx.addRow(...)
// 尝试找到一个精确覆盖dlx.solve()
求解数独问题
¶数独是精确覆盖问题的一个特例。为了套用 DLX 算法框架,首先需要弄清楚如何构建 $01$ 矩阵。一般来说,可以将列对应成约束,而将行对应到策略,即选择某个策略时能够满足哪些约束。比如考虑经典 $x^2 \times x^2$ 数独游戏,其有如下类型的约束:
- $Slot(a,b)$: 第 $a$ 行第 $b$ 列格子要有数字;
- $Row(a,b)$: 第 $a$ 行要有数字 $b$;
- $Col(a,b)$: 第 $a$ 列要有数字 $b$;
- $Sub(a,b)$: 第 $a$ 个子方阵中要有方阵 $c$;
一共有 $x^2 \times x^2 \times 4$ 中约束。再考虑可选择的策略,即在第 $r$ 行第 $c$ 列填入数字 $v$,且可以满足约束 $Slot(r,c)$、$Row(r,v)$、$Col(c,v)$、 $\displaystyle Sub\left(\left\lfloor \frac{r}{x} \right\rfloor \times x + \left\lfloor \frac{c}{x} \right\rfloor,v\right)$。
代码如下:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283import { createDLX } from './dlx'
/** * Sudoku constraints. */export enum SudokuConstraint { SLOT = 0, // Slot(a, b) 表示第 a 行 b 列个格子上要有数字 ROW = 1, // Row(a, b) 表示第 a 行要有数字 b COL = 2, // Col(a, b) 表示第 a 列要有数字 b SUB = 3, // Sub(a, b) 表示第 a 个子方阵要有数字 b}
export interface SudokuSolver { /** * 数独的谜题格子,从 0 开始填,若某个格子未被填,则将其置为 -1 * @param puzzle */ solve(puzzle: number[][]): boolean}
/** * @param SUDOKU_SIZE_SQRT 数独子方阵大小(即数独行数的平方根) */export function createSudokuSolver(SUDOKU_SIZE_SQRT: number): SudokuSolver { const ebs = 1e-6 const SUDOKU_SIZE = SUDOKU_SIZE_SQRT * SUDOKU_SIZE_SQRT const SUDOKU_SIZE_SQUARE = SUDOKU_SIZE * SUDOKU_SIZE const MAX_NODES = SUDOKU_SIZE_SQUARE * 4
let codeA: number, codeB: number, codeC: number const columns: number[] = new Array<number>(4) const solver = createDLX(MAX_NODES) return { solve }
function solve(puzzle: number[][]): boolean { solver.init(MAX_NODES) for (let r = 0; r < SUDOKU_SIZE; ++r) { for (let c = 0; c < SUDOKU_SIZE; ++c) { const w = puzzle[r][c]
// (r,c) 所属的子方阵编号 const s = Math.floor(r / SUDOKU_SIZE_SQRT + ebs) * SUDOKU_SIZE_SQRT + Math.floor(c / SUDOKU_SIZE_SQRT + ebs) for (let v = 0; v < SUDOKU_SIZE; ++v) { if (w === -1 || w === v) { columns[0] = encode(SudokuConstraint.SLOT, r, c) columns[1] = encode(SudokuConstraint.ROW, r, v) columns[2] = encode(SudokuConstraint.COL, c, v) columns[3] = encode(SudokuConstraint.SUB, s, v) solver.addRow(encode(r, c, v), columns) } } } }
const answer: number[] | null = solver.solve() if (answer === null) return false
for (const code of answer) { decode(code) // eslint-disable-next-line no-param-reassign puzzle[codeA][codeB] = codeC }
return true }
function encode(a: number, b: number, c: number): number { return a * SUDOKU_SIZE_SQUARE + b * SUDOKU_SIZE + c + 1 }
function decode(code: number): void { let c = code - 1 codeC = c % SUDOKU_SIZE
c = Math.floor(c / SUDOKU_SIZE + ebs) codeB = c % SUDOKU_SIZE
c = Math.floor(c / SUDOKU_SIZE + ebs) codeA = c }}
我把求解数独的算法封装在了 @algorithm.ts/sudoku 中,下面是求解 $3^2 \times 3^2$ 数独谜题的示例[5]:
Related
¶- 刘汝佳《算法竞赛入门经典──训练指南》 P406 6.3.3 精确覆盖问题和 DLX 算法