网络流基础之最大权闭合图
Terms
¶对于有向图 $G=(V,E)$，其中 $V$ 为 $G$ 的点集，$E$ 为 $G$ 的边集。
割集: 一个 $s-t$ 割 $[S,T]$ 是 $V$ 的一种划分，使得 $s\in S$、$t\in T$
最小割: 一个 $s-t$ 割的容量是 $\displaystyle c(S,T) = \sum_{(\mu,\nu) \in (S\times T)\bigcap E} c(\mu,\nu)$；容量最小的割集称为最小割
简单割：若一个 $s-t$ 割满足割中的每条边都只与源点 $s$ 或汇点 $t$ 相连，则称该割为简单割
闭合图：若点集 $V' \in V$ 是一个闭合图，那么对于 $\forall \left< \mu, \nu\right > \in E$，若 $\mu \in V'$ 则必有 $\nu \in V'$
最大权闭合图： 一个点权和最大的闭合图
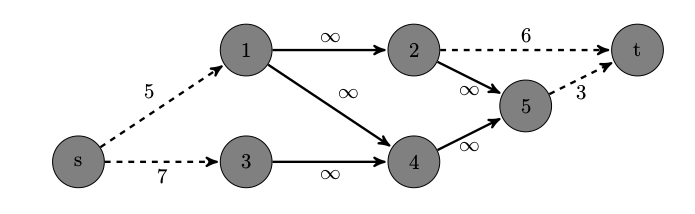
如下图所示，图中有 9 个闭合图（含空集）：$\emptyset$，$\lbrace 3,4,5 \rbrace$， $\lbrace 4,5 \rbrace$，$\lbrace 5 \rbrace$，$\lbrace 1,2,4,5 \rbrace$， $\lbrace 2,5 \rbrace$，$\lbrace 2,4,5 \rbrace$，$\lbrace 2,3,4,5 \rbrace$， $\lbrace 1,2,3,4,5 \rbrace$。其中，惟一的最大权闭合图为 $\lbrace 3,4,5 \rbrace$，且权和为 $4$
最大流最小割定理
¶设 $f$ 为流网络 $G=(V,E)$ 中的一个流, 该流网络的源节点为 $s$, 汇点为 $t$, 则下面的条件是等价的:
- $f$ 是 $G$ 的一个最大流
- 残流网络 $G_f$ 不包含任何增广路径
- $|f|=c(S,T)$, 其中 $[S,T]$ 是流网络 $G$ 的最小割
网络流与最大权闭合图
¶将原图转化为网络 $N=(V_N, E_N)$：
将原图中的所有有向边 $\left< \mu, \nu\right > \in E$ 替换为容量为 $c(\mu,\nu)=\infty$ 的有向边 $\left< \mu,\nu \right>$，并将其纳入边集 $E_N$
增加源点 $s$ 和汇点 $t$
由源点向原图中的所有正权点 $\nu(\omega_\nu > 0)$ 连接一条容量为 $c(s,\nu)=\omega_\nu$ 的有向边 $\left< s,\nu \right>$，并将其纳入边集 $E_N$
由原图中的所有负权点 $\nu(\omega_\nu < 0)$ 连接一条容量为 $c(\nu,t)=-\omega_\nu$ 的有向边 $\left< \nu,t \right>$，并将其纳入边集 $E_N$
也就是
上式中的 $\infty$ 取一个大于 $\displaystyle \sum_{\nu \in V} \big| W_\nu \big|$ 即可。则原图 $G$ 构成的网络 $N$ 如下图
若原图所有正权点的点权和为 $R_v$，对该网络跑最大流，且最大流为 $R_f$，所得到的最小割为 $[S,T]$，则有：
原图的最大权闭合图的权和为 $R_v-R_f$
$S-\lbrace s \rbrace$ 为原图点数最少的最大权闭合图
证明由下述几个引理构成。
引理1
¶本问题的网络 $N$ 中，最小割是简单割。
由于除与源点 $s$ 或汇点 $t$ 直接相连的边的容量是有限的，其它边是无限的，那么最小割中显然不会出现容量为无限的边（因为强行割断所有与源点相连的边可以构成一个割集，且割的容量是有限的，最小割的容量不会比这个大），所以该最小割是简单割。
引理2
¶记 $G_1$ 是原图 $G$ 的一个闭合子图，$V_1$ 为 $G_1$ 的点集；$\overline{V_1}$ 为点集 $V_1$ 在原图 $G$ 中的补集，即 $V_1 \bigcup \overline{V_1}=V$。则网络 $N$ 的简单割 $[S,T]$ 与图 $G$ 的闭合子图 $G_1$ 存在一个一一对应关系：
其中
闭合图对应简单割：即 $S=V_1 \bigcup \lbrace s \rbrace$，$T=\overline{V_1} \bigcup \lbrace t \rbrace$
因为 $V_1$ 是一个闭合图，所以不存在 $\left< \mu,\nu \right> \in E$，其中 $\mu \in S-\lbrace s \rbrace$，$\nu \in T-\lbrace t \rbrace$。也就是不存在不与源汇有关联的边，其两个端点分别在 $V_1$ 和 $\overline{V_1}$ 中，所以 $[S,T]$ 是一个割集。
由 引理1 可知，$[S,T]$ 是一个简单割。简单割对应闭合图：即 $V_1=S-\lbrace s \rbrace$ 是一个闭合图。
若 $\mu \in S-\lbrace s \rbrace$，$\nu \in T-\lbrace t \rbrace$；显然不存在边 $\left< \mu,\nu \right> \in E$，否则与 $[S,T]$ 是割集矛盾（因为 $c(\mu,\nu)=\infty$）。
引理3
¶记 $V^+$ 为 $V$ 中点权为正的最大点集，$V^-$ 为 $V$ 中点权为负的最大点集；类似地，定义 $V_1^+$、$V_1^-$、$\overline{V_1}^+$、$\overline{V_1}^-$. 则在 引理2 的一一对应关系下（即 $V_1\bigcup\lbrace s \rbrace=S$、$\overline{V_1}\bigcup\lbrace t \rbrace=T$），有：
显然，$\displaystyle \Big[S,T\Big] = \left[\lbrace s\rbrace,\overline{V_1}\right] \bigcup \Big[\lbrace t\rbrace,V_1\Big] \bigcup \left[\overline{V_1},V_1\right]$ （分析构造图的源汇关联情况不难得出结论）
- 因为$[S,T]$ 是简单割，故 $\displaystyle \left[\overline{V_1},V_1\right] = \emptyset$
- 又因为 $s$ 只与正权点连边，故 $\displaystyle \left[\lbrace s\rbrace,\overline{V_1}\right] = \left[\lbrace s\rbrace,\overline{V_1}^+\right]$
- 而 $t$ 只与负权点连边，故 $\displaystyle \left[\lbrace t\rbrace,V_1\right] = \left[\lbrace t\rbrace,V_1^-\right]$ 因此，$\displaystyle \Big[S,T\Big] = \left[\lbrace s\rbrace,\overline{V_1}^+\right] \bigcup \Big[\lbrace t\rbrace,V_1^-\Big]$，即可证明了式 $(1)$ 的正确性
引理4
¶当网络 $N$ 取得最小割时，其对应的图 $G$ 的闭合图（$V_1=S-{s}$）将取得最大权（最优性）：
按照定义，闭合图的权值为正权点的权的绝对值和 - 负权点的权的绝对值和，即
$$\omega(V_1) = \sum_{\nu\in V_1^+}\omega_\nu - \sum_{\nu\in V_1^-}(-\omega_\nu) \tag{2}$$由式 $(1)$ 和式 $(2)$，可得：
$$\begin{align} \omega(V_1) + c[S,T] &= \sum_{\nu\in V_1^+}\omega_\nu - \sum_{\nu\in V_1^-}(-\omega_\nu) + \sum_{\nu\in \overline{V_1}^+} \omega_\nu + \sum_{\nu\in V_1^-} \left( -\omega_\nu \right) \\ &= \sum_{\nu\in V_1^+}\omega_\nu + \sum_{\nu\in \overline{V_1}^+} \omega_\nu \\ &= \sum_{\nu\in V^+} \omega_\nu \end{align}$$整理得 $\displaystyle \omega(V_1) = \sum_{\nu\in V^+}\omega_\nu - c[S,T]$
Related
¶- 《最小割模型在信息学竞赛中的应用》--by 胡伯涛